Proof of a syntactic sequent: example

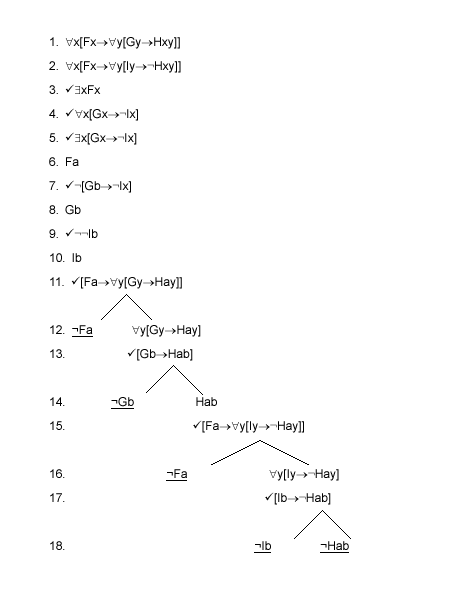
We will prove the following sequent:

            "x[Fx®"y[Gy®Hxy]], "x[Fx®"y[Iy®¬Hxy]], $xFx |- "x[Gx®¬Ix]

The counterexample set is

            {"x[Fx®"y[Gy®Hxy]], "x[Fx®"y[Iy®¬Hxy]], $xFx, ¬"x[Gx®¬Ix]}

In constructing the tableau we will put in ticks  (but remember that they are entirely optional) and line numbers (for ease of reference).

Comments:

Lines 1-4: these are the members of the counterexample set.

Line 5: from line 4 by the ¬"xj rule. We could have done the $xj rule on line 3 instead; we can't however apply the "xj rule to lines 1 and 2 until we have some designators in the branch.

Line 6: from line 3 by the $xj rule.

Line 7: from line 5 by the $xj rule. (We could have applied the "xj rule to line 1 or 2; but it is sensible usually to make $xj applications first, since they supply new designators from which we can make a choice when using the "xj rule.)

Lines 8-10: We might as well apply these propositional rules while we are about it to simplify things.

Line 11: Application of the "xj rule to line 1. It looks as if using "a" may help, since we have "Fa" in line 6.

Line 12: Using "a" in line 11 did help. Notice that it meant that the left branch closed, and in effect we got ""y[Gy®Hay]" from lines 6 and 11. In general, when we have "j" in one line and "[j®y]" in another we can get "y", because when we apply the [j®y] rule the left branch closes.

Line 13: this time it looks sensible to use "b", because we have "Gb" in line 8.

Line 14: and we get Hab.

Line 15: We apply the "xj rule to line 2: using "a" seems sensible again, given "Fa" in line 6.

Line 16: and we get ""y[Iy®¬Hay]"

Line 17: This time using "b" is a good idea, because of the "Ib" in line 10.

Line 18: and we get "¬Hab"; and the right branch closes as well. Actually we notice that the left hand branch would have closed because of the presence of "¬¬Ib" in line 9: so we didn't actually need line 10 at all.

The tableau closes. So the sequent is correct.