The $xj rule

The rule is:

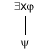where there is a proper name D which has not occurred anywhere in the branch to which y is added, and y is the result of replacing each free occurrence of "x" in j by an occurrence of D.

Note particularly:

1. "D" must be new to the branch;

2. "D" must be a proper name;

3. The rule applies only to formulae which begin with "$".

The rationale for the rule is that if a predicate is true of something, we won't introduce any inconsistency by naming something it is true of, as long as we have not already used the name for some purpose.

Notice particularly that the y which we add does not follow from "$xj". The position rather is that, if the branch containing "$xj" is not inconsistent, we shall not introduce any inconsistency by adding "y" to it, provided that "D" does not already occur in the branch. So, if an inconsistency appears as a result of adding "y", the formulae in the branch must already have been inconsistent. In other words, even though "y" does not follow from "$xj", adding it may help to reveal an inconsistency which is already latent.

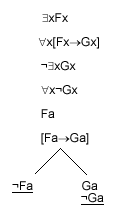
Example: a proof that the following argument is valid:

The counterexample set is {$xFx, "x[Fx®Gx], ¬$xGx}.

The tableau closes; so the counterexample set is inconsistent; so the argument is valid.

The following are incorrect:

(i) An attempt to prove that {$xFx, $x¬Fx} is inconsistent:

The application of the rule to add "Fa" was correct; but the application to add "¬Fa" was not, because "a" was not new to the branch.

(ii) An attempt to prove that "$xFx" follows from ""xFx". (It doesn't if we are allowing for the possibility of an empty domain, because in the empty domain ""xFx" is true, but "$xFx" is false.)

The mistake consists in applying the rule to a formula which does not begin with "$".

The following is correct:

And at this stage there is nothing worthwhile we can do. We can't apply the "xj rule because we have no designators in the branch.

(iii) An attempt to prove that there are no white cows.

Our interpretation is:

Domain: everything

Cx:       x is a cow

Wx:      x is white

a:          Farmer Jones's brown cow

b:         Buttercup

We formalise "There are some white cows" as "$x[CxÙWx]". And we construct a tableau thus:

The tableau does not close, but referring back to the interpretation, we see that "Wa" formalises "Farmer Jones's brown cow is white". But, we reason, this is a contradiction. So the open branch is, after all, impossible. So "$x[CxÙWx]" is inconsistent. So there are no white cows. The mistake consisted in the fact that we introduced "a", which is not a proper name. And one can see that the rule rightly requires us to use a proper name – the reason is that there is a risk with other designators that information may already be associated with them, even if they have not been used already.

The following is correct:

Again, of course, the tableau does not close; but this time reference back to the interpretation reveals no inconsistency in "Wb".