3: Propositional Calculus:

Tableaux

Sentence Tableaux

Sentence tableaux provide us with a way of telling whether a set of sentences is consistent or not. They work in effect by breaking down sets of complex sentences into sets of simpler sentences where inconsistency is easier to spot.

Let us investigate the consistency of the following set of sentences:

            John likes rugby if he is Welsh

            John is Welsh unless his father is Scottish

            John's father is Welsh but John does not like rugby.

We proceed as follows:

Step 1: Translate the English sentences using the truth-functors of the propositional calculus. (Remember to use stand-alone sentences for the constituents.)

This gives us:

            [John is Welsh ® John likes rugby]

            [John is Welsh Ú John's father is Scottish]

            [John's father is Welsh Ù ¬John likes rugby]

Step 2: Abbreviate the short constituent English sentences with single capital letters.

Let us abbreviate them thus.

W:        John is Welsh

L:         John likes rugby

F:         John's father is Welsh

S:         John's father is Scottish

This key is called an interpretation. The capital letters are called sentence letters.

This gives us:

            [W®L]

            [WÚS]

            [FÙ¬L]

In each case the resulting combinations of letters and truth-functors is a formula, (sometimes called a "wff": i.e. well formed formula; pronounced "woof".); the process of translating into formulae is formalisation.

Normally one can perform the first two steps simultaneously.

The tableau takes the form of an upside down tree, with the original formulae constituting the trunk. The rules tell us

Each path from root to tip is called a "branch". So each branch actually includes the trunk.

Each such branch, until it is closed, (actually, as we shall see, the unticked formulae in each such branch) represents a way in which the original sentences might perhaps be true. And closing a branch signifies that this branch is not after all a way in which the original sentences could all be true. So if all the branches close, that means that there was no way in which the original sentences could all be true; that is, that they are inconsistent.

There is just one rule for closing a branch: we may close a branch just if it contains both a formula and the same formula with a "¬" in front (each as a whole line in the branch). That is to say, a branch closes just if it contains both "j" and "¬j" for some j. To close a branch we just underline the tip.

There is a rule for extending any branch containing a formula of the form ¬¬j. There is a rule for extending a branch containing a formula of the form [jÙy], and another for a branch containing a formula of the form ¬[jÙy]. And so on for each of the 2-place truth-functors (a rule for a formula of that form, and another rule for the corresponding negated formula). There is no rule that can be applied to a formula which consists of just a sentence letter - "P", for instance; and none that can be applied to a formula which consists of just a negated sentence letter - "¬P", for instance.

Notice that each of these rules applies only to a formula which occupies the whole line in the branch. So if a line consists of [¬[PÙQ]Ú¬¬R] one can apply the rule for [jÚy], but no other rule (to this formula). There is at most one rule that can be applied to a given formula.

Let us now construct a tableau for our example. First the trunk:

Now we could apply the [j®y] rule to the first formula, or the [jÚy] rule to the second formula, or the  [jÙy] rule to the third formula. It doesn't matter which. Let us apply the  [jÚy] rule to the second formula.

This rule tells us that we can turn each open branch in which our formula occurs into two branches, one with "j" at its tip, and the other with "y" at its tip.

This is reasonable, because there are two ways in which "[jÚy]" can be true: it will be true if "j" is true and it will be true if "y" is true. The rule also tells us to tick the formula to which the rule is applied. This tells us not to apply a rule again to this line. (This would certainly be a waste of time if it were allowed, since we would have to apply the same rule again; and that would simply give us branches identical to those with already had, apart from some repetition.)

We apply the rule like this:

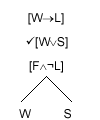After each application of a rule for extending branches, we check whether we can close a branch. We can't yet.

We started with a set of formulae which might perhaps all be true. What our tableau so far tells us (in effect) is that there are two ways in which the original formulae might all be true. One way would be for "[W®L]", "[FÙ¬L]" and "W" all to be true; and the other way would be for "[W®L]", "[FÙ¬L]" and "S" all to be true.

Let us now apply the [jÙy] rule to "[FÙ¬L]". This rules tells us that to each open branch in which our formula occurs we can add "j" and "y". This is reasonable, since there is just one way in which "[jÙy]" can be true: if "j" and "y" are both true. Again we tick our formula. The tableau now looks like this:

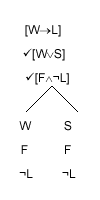Again we check to see if a branch will close. None will.

Our tableau now, in effect, tells us that there are two ways in which the original sentences might all be true: if "[W®L]", "W", "F" and "¬L" are all true, and if "[W®L]", "S", "F" and "¬L" are all true.

We now apply the [j®y] rule to "[W®L]". This tells us that we can turn each open branch in which our formula occurs into two branches, one with "¬j" at its tip, and the other with "y" at its tip. This is reasonable, because there are two ways in which "[j®y]" can be true: it will be true if "j" is false and it will be true if "y" is true; that is to say, it will be true if "¬j" is true and it will be true if "y" is true. Again we tick.

We now have:

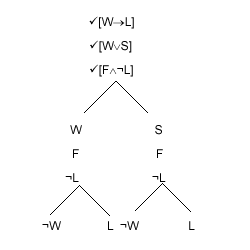This time we can close some branches.

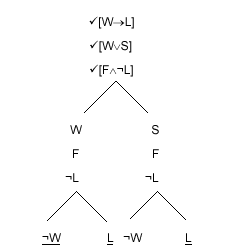Closing a branch tell us that this branch does not after all represent a way in which the original sentences could all be true; because there is no way for "j" and "¬j" both to be true. We now have just one open branch. So the tableau now tells us that there is just one way in which the original sentences could all be true. They would be true if the following were all true: "S", "F", "¬L" and "¬W".

At this stage we can develop the tableau no further, since the unticked formulae in the open branch are all either sentence letters or negated sentence letters. If the branches were all closed, we could, of course, conclude that the original sentences could not all be true. But the fact that we have an open branch and the tableau has finished does not tell us that the sentences could all be true.

First we must go back to our interpretation to see if the unticked formulae in our open branch could in fact all be true. So we need to decide whether the following could be true together: "John's father is Scottish", "John's father is Welsh", "John does not like rugby" and "John is not Welsh". Perhaps we will reckon that it is impossible to be both Welsh and Scottish. In which case we will say that these cannot be true together; so nor can the original sentences; so the original set is inconsistent.

Perhaps we will reckon that if one's father is Welsh, one must be Welsh as well. In which case again we will conclude that the original set is inconsistent. Otherwise, presumably, we will conclude that the original set is consistent.