Ticking

When we constructed propositional tableaux, and we applied a rule to some formula "j", we added the new formula or formulae to every open branch in which "j" occurred, and we ticked the formula "j". This signified that there was nothing further to be extracted from "j"; the unticked addition represented all the information which "j" contained.

The rules for predicate tableaux do not call for ticking, however. This is because we are allowed to apply the same rule to the same formula more than once; and sometimes we need to. And the absence of the requirement to tick also means that, when we apply a rule to "j", we are not obliged to add the new formula or formulae to every open branch in which "j" occurs. And sometimes we may not want to, because to do so will not help.

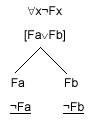
Here is a simple example of a case where we not only may, but need to, apply the same rule to the same formula more than once:               

Notice that we needed to apply the "xj rule once to get "¬Fa" and again to get "¬Fb". Notice also that there was no point in adding "¬Fa" to the right branch; though it would have been perfectly permissible to do so.

In spite of the fact that the rules do not require ticking, you may well find that it is useful to tick in the following cases, if only as a piece of book-keeping:

when you apply a propositional rule to "j", as long as you have added the new formula(e) to every open branch in which "j" occurs;

when you apply the ¬$xj rule or the ¬"xj rule, as long as you have added the new formula to every open branch which contains the relevant occurrence of "¬$xj" or "¬"xj".;

when you apply the $xj rule, as long as you have added the new formula to every open branch which contains the relevant occurrence of "$xj". (It is true that a second application of the rule will give one something new in the branch or branches; for instance two applications to "$xFx" might give one both "Fa" and "Fb"; but this will never help. If one can get the tableau to close with two applications, one could also have got it to close with just one.)

In fact the only rule (of those we have met so far) which can profitably be applied twice to the same formula, is the "xj rule.