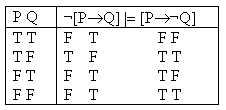Exercise 3.1 - Answers
1 |
(i) |
Correct 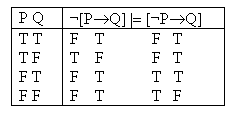
The
only structure which makes ¬[P®Q] true (the second row) makes [¬P®Q]
true too. |
|
(ii)
|
Correct
The only structure which makes ¬[P®Q] true (the second row) makes [P®¬Q] true too. |
|
|
(iii)
|
Incorrect. 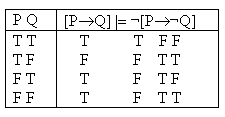 Rows
three (P is false and Q is true) and four (P is false and Q is false)
both provide counterexamples. |
|
|
(iv)
|
Correct. 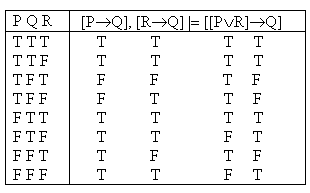
It
is easiest here to look at the rows in which the formula after the
turnstile is false. There are three, and in each of them at least
one of the formulae before the turnstile is false too. (In the third
row both are false; in the fourth row [P®Q]
is false; in the seventh row [R®Q] is false.) So there is no structure in
which all the formulae before the turnstile are true and the formula
after it is false. |
|
|
(v)
|
Incorrect. 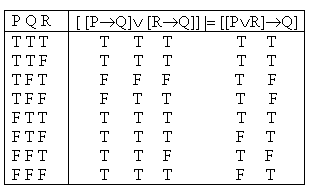
Rows three (P is true, Q is false, R is true) and seven (P is false, Q is false, R is true) both provide counterexamples.
|
|
|
|
(vi) |
Incorrect. The
structure where P is false and Q is true is a counterexample. So
is the structure where P is true and Q is false. |
|
|
(vii) | Correct |
| (viii) | Correct.
(Any sequent whose premises are inconsistent is correct. This corresponds
to the fact that any argument with inconsistent premises is valid.) |
|
| (ix) | Correct.
(Any sequent whose conclusion is a semantic theorem – i.e. is never
false – is correct. This corresponds to the fact that any argument
whose conclusion is a necessary truth is valid.) |